Sean Dae Houlihan

Emotion prediction as computation over a generative theory of mind

Emotion prediction as computation over a generative theory of mind

Computed Appraisals

Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences

Sean Dae Houlihan
MIT
Max Kleiman-Weiner
Harvard, MIT
Luke Hewitt
MIT
Josh Tenenbaum
MIT
Rebecca Saxe
MIT
 Paper  Code
Correction
The journal publication includes a graphical error in Figure 6(a). The Inverse Planning Lesion model incorrectly shows arrows from beliefs $(\pi)$ and preferences $(\omega)$ to a player's action $(a_1)$. The model is correctly described in the text and correctly depicted in the Supplementary Materials (Figure S7).
The graphical error has been fixed in the corrected PDF (also linked above).

Motivation

How do people predict what emotions others will experience?

To study this remarkable feat of everyday social intelligence, we frame emotion prediction as causal reasoning over a Bayesian Theory of Mind.

Most research focuses on how people infer emotions from others’ expressions, so why study emotion prediction?

A large body of work has shown that observers use predictions of what emotions others are likely to experience in order to interpret their expressions.

In addition, a huge part of human life involves planning our actions based on how we predict that others will react.

So if we want to understand human social cognition, and build social machines that interact with people, modeling emotion prediction is key.

The present aim is to model how observers reason about event information when predicting what emotions others will experience. As such, this work presents a model of observers’ social cognition, not a model of people’s actual emotions.

Overview

Humans can predict others’ emotional reactions because we have an “intuitive theory” (a mental model) of the causal relationships between emotions, events, preferences, beliefs, intentions, actions, etc.

We intuitively understand that people enjoy getting things they want, and that different people want different things. That getting something expected feels different than getting the same thing without expecting it. That getting $5 is great when the alternative is $0, but not so great when the alternative is $100.

k9 counterfactual

Modeling human emotion understanding is a challenge. People’s conceptual knowledge of emotions is hard to specify by hand, and hard to learn from observation.

In this paper, we show how causal models can reverse-engineer people’s intuitive theory of emotion.

Causal Model of Emotion Prediction

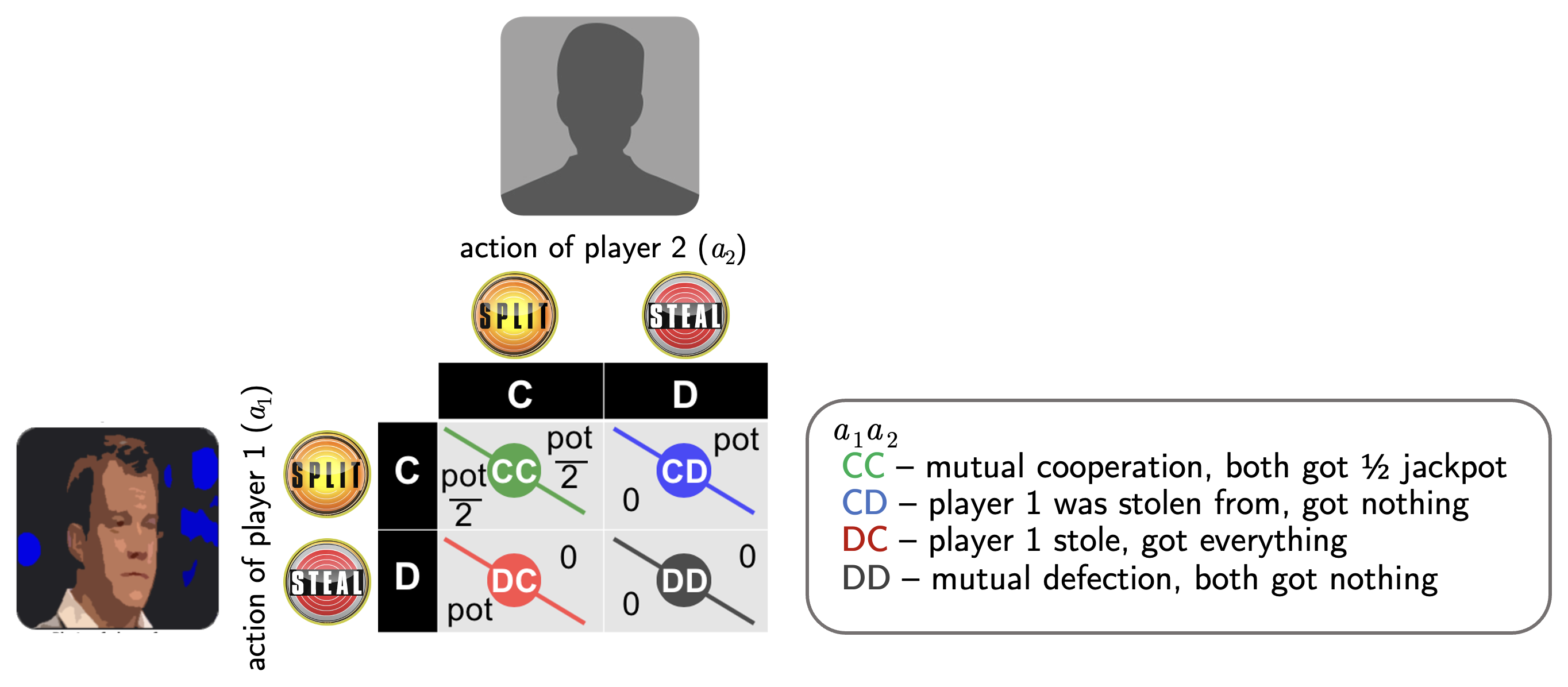
Observers were given descriptions of people playing a public one-shot prisoner’s dilemma and predicted the people’s emotional reactions to the outcome of the game. The rules were based on the British TV game show, Golden Balls.

Payoff Matrix

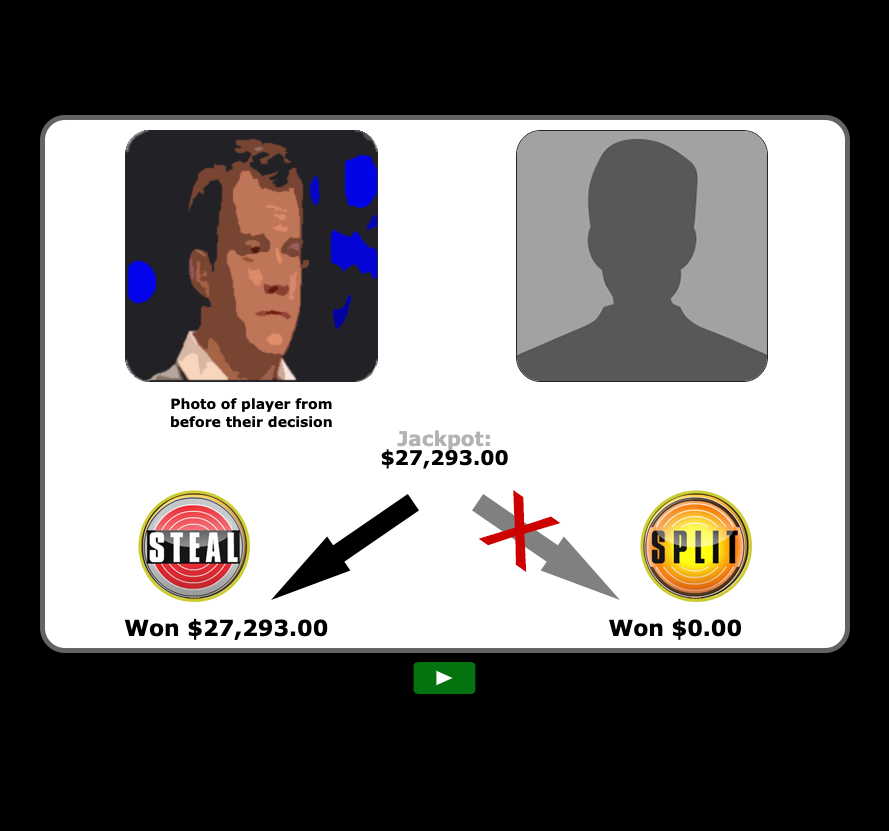
Observers predicted a player’s emotions based on information about what happened (the target player’s action, the opponent’s action, the size of the jackpot, and how much the two players won). Note that observers were shown a photo of a player’s face from before the game but never saw the expressions a player made in reaction to the game’s outcome.

expt1 expt2

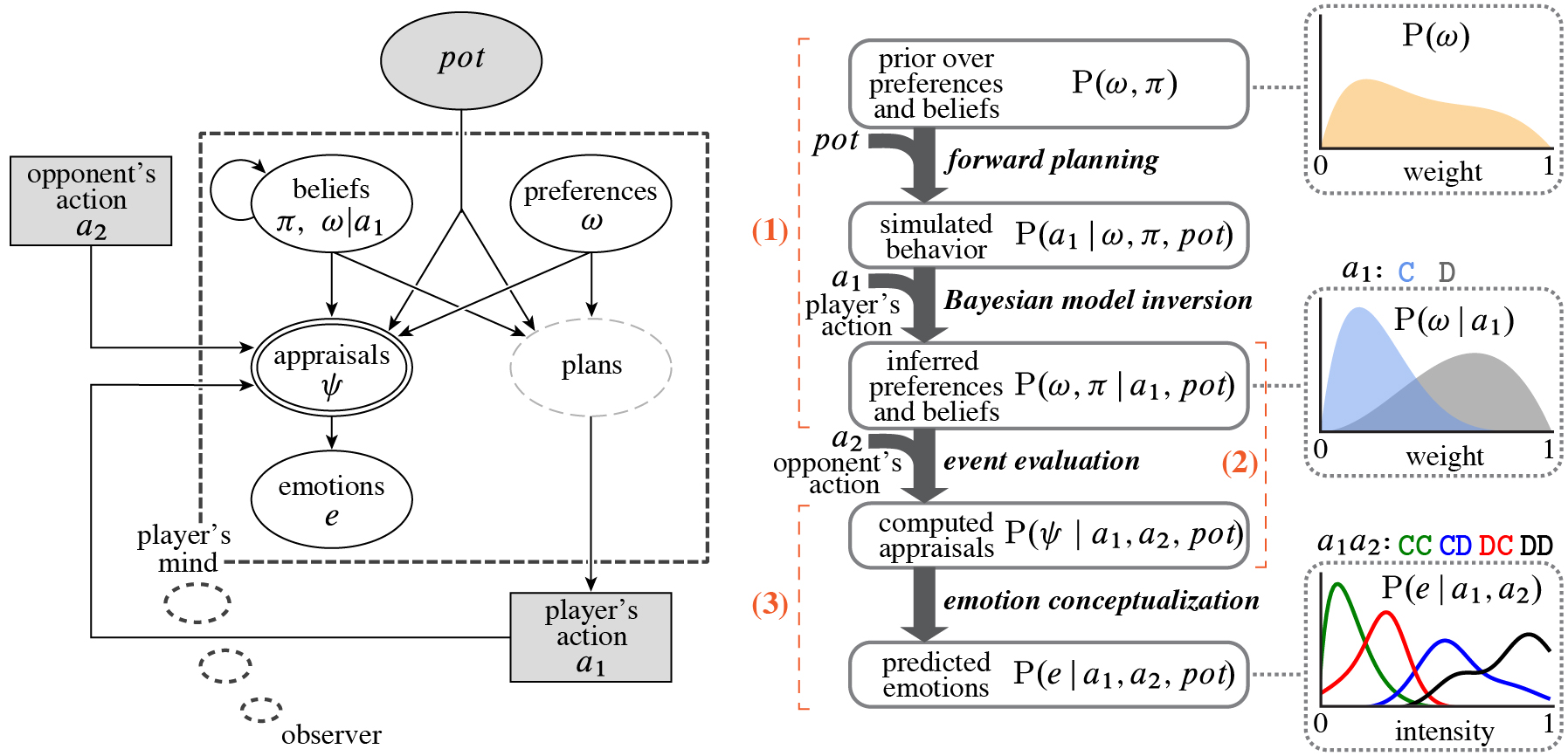
Building a formal model that can reason about players’ emotional reactions based on an event description requires rich computational structure. We integrate ideas from inverse planning, behavioral economics, (reverse-) appraisal theory, and constructivist theories of emotion.

We describe the model in three Modules.

ModuleDescriptionSimulated Cognition
1inverse planninginfer mental contents (preferences and beliefs) given a player’s action
2appraisal computationreason about how a player will appraise an event with respect to the inferred mental contents
3emotion conceptualizationpredict a player’s emotions based on the computed appraisals

Module 1: inverse planning

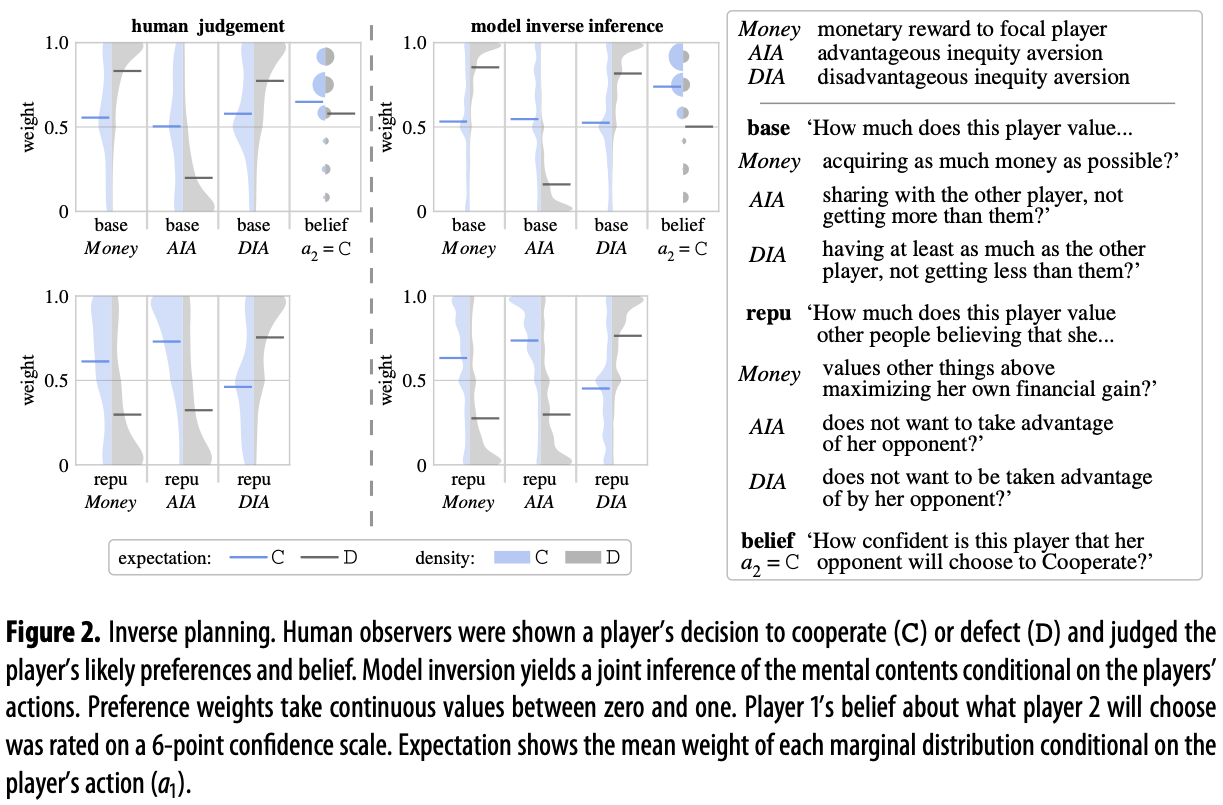
Module 1 recursively inverts increasingly complex generative models of players’ behavior. This enables the model to infer what unobserved mental contents were likely to have motivated a player, given the action that the player was observed to choose.

module1

We compare the model’s inverse inference to an independent group of observers, who made similar inferences about players’ mental contents. E.g. players who cooperate are inferred to be less greedy, to desire a prosocial reputation, and to expect their opponents to also cooperate.

fig2

Module 2: appraisal computation

Module 2 computes players’ appraisals — how observers think that a player will evaluate the outcome of the game, based on the player’s mental contents.

We extend the idea of “inverse planning” to generate probabilistic representations of players’ reactions to new world states.

module2

We compute subjective utilities, prediction errors, and multiple types of counterfactuals over players’ inferred preferences and beliefs. This yields a rich space of “computed appraisals”.

computed appraisals

Module 3: emotion conceptualization

Module 3 learns “emotion concepts” — functions that translate computed appraisals to continuous intensities of 20 emotions.

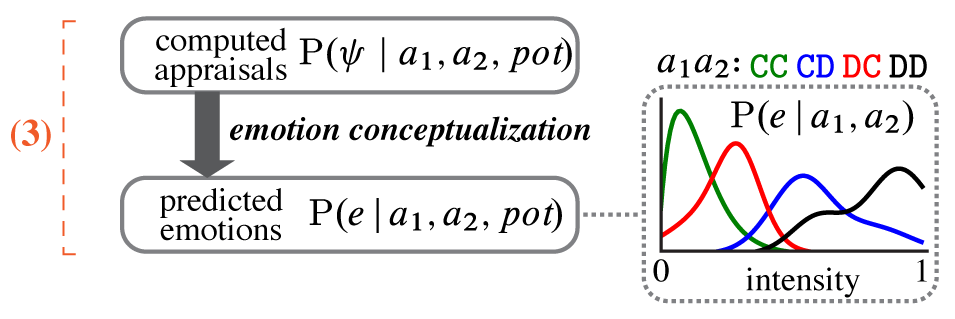
module3

Since the joint distribution of computed appraisals is designed to recapitulate observers’ latent reasoning about players’ minds, we can constrain the function learning using the generative structure of the model.

fig3

This yields a “computational appraisal theory.”

In effect, we learn the computational structure of people’s intuitive theory of emotion, directly from observers’ emotion judgments.

fig4

The learned functions reflect the sophistication of observers’ latent Theory of Mind reasoning. The computed appraisal variables (and the learned emotion concepts) are interpretable owing to the cognitive structure of the generative model.

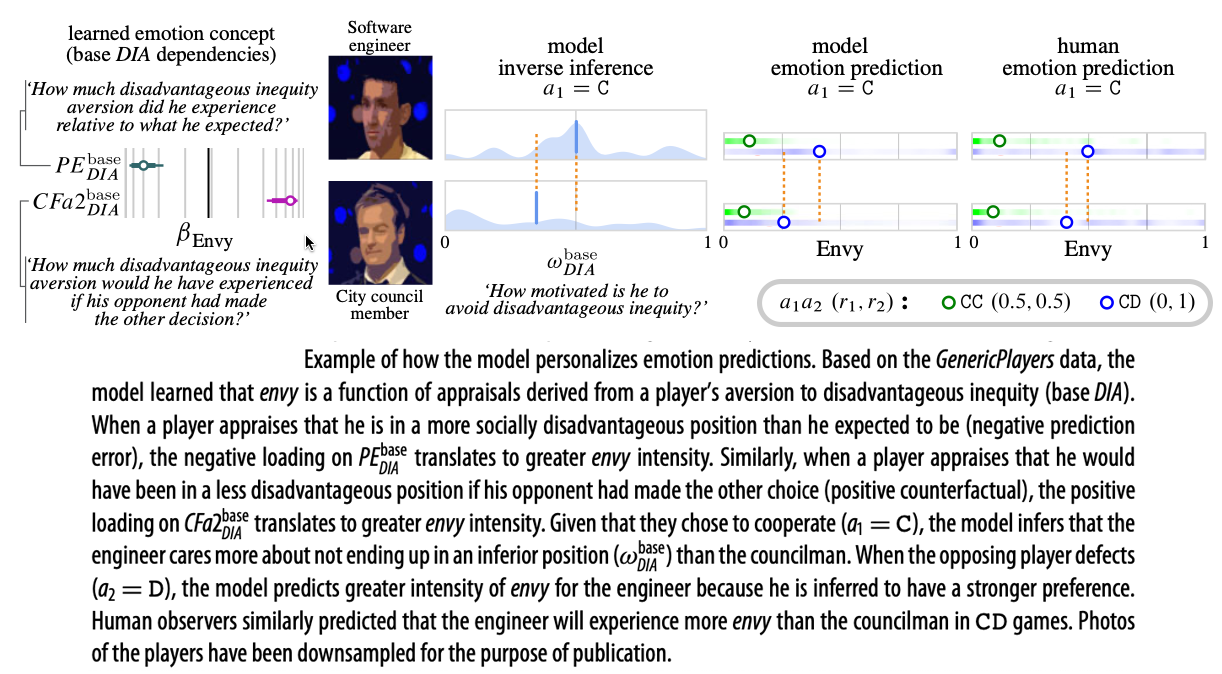
Personalization

Since the model is Bayesian, it depends on priors. This offers a way to test if the model responds to prior information like humans.

We gave observers brief personalizing descriptions of specific players (e.g. “software engineer at Google”, “city council member about to start campaigning for State Senate”). One group rated the specific players’ motivations, another group rated emotions.

Ratings of a specific player’s motivations were used to form a personalized prior. Using this prior, the model generated predictions of that player’s emotional reactions to various events (if the player split a jackpot of $694, if the opponent stole $61,430, etc.).

The model predicted how the personalizing information would bias observers’ emotion predictions. E.g., because the “software engineer” was inferred to care more about not being taken advantage of, the model predicted that observers would expect him to experience more envy, which they did.

fig5

Lesion models

Finally, we compare our model to simpler alternatives.

The Golden Balls game is highly constrained (two people, binary choices, a pot size).

And this model is elaborate, involving counterfactuals over recursive inverse inferences of social preferences, etc.

But the rich model structure is necessary to capture human social cognition, even in this simple game.

Lesioning inverse planning, or lesioning social preferences, impairs the capture of specific emotions.

fig6 1

And both lesions impair the model’s ability to update emotion predictions for specific players based on personalizing prior information.

fig6 2

Reflections

This work has wholly transformed how I think about modeling the mind.

It has also been an ideal collaboration in that it built on, and extended, prior work from all of the coauthors to do something we all imagined was possible.



Press

MIT News: Computational model mimics humans’ ability to predict emotions



Authors’ Twitter Threads

×

Cite

@article{houlihan2023computedappraisals,
  title = {Emotion Prediction as Computation Over a Generative Theory of Mind},
  author = {Houlihan, Sean Dae and Kleiman-Weiner, Max and Hewitt, Luke B. and Tenenbaum, Joshua B. and Saxe, Rebecca},
  date = {2023},
  journaltitle = {Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences},
  shortjournal = {Phil. Trans. R. Soc. A},
  volume = {381},
  number = {2251},
  pages = {20220047},
  doi = {10.1098/rsta.2022.0047},
  url = {https://royalsocietypublishing.org/doi/10.1098/rsta.2022.0047}
}